Super Full-Wave Octaver
(c) JC Maillet (2005)
Ever wonder what F(x) = |x| sounds like ? Of course I'm speaking in terms of the DC-Transfer function of a non-linear wave-shaper circuit ... for those who don't know Spice or network theory very well - this transfer maps out the quasi-static change in DC conditions everywhere in the circuit (currents and voltages) as the input source (current or voltage) changes in same manner ... this mapping, I should add, totally ignores the frequency dependent behavior of the circuit - it's doing the test at DC (0hz) ... this stuff is routinely used to uncover the harmonics generating capability of non-linear analogue gain stages ...
Full-wave rectifiers are known to be described ideally by the absolute value function usually written as abs(x) or |x| ... most full-wave rectifiers use diodes and depending how they are wired can rob the |x| function of accuracy in the viscinity of the origin (0v)
The following Full-Wave circuit comes from the super-diode class of op-amp circuits - it's a circuit block I found inside an old compressor design ... it achieves a |x| to a very low voltage value (probably to the order of the diode turn-on voltage (0.7) divided by the open-loop gain of the op-amp (1e6) - basically well below the grass ... the first schematic below shows how the circuit can be wired for perfectly symmetic half-cycles ... after you've built it notice how fizzy the octave output sounds ... what's happening here is you're getting a highest possible number of (high) Fourier terms by the fact the approximation to |x| is going "virtually" down to 0v [Note: a sharp corver in a DC-Transfer function gives way to a high orders of upper harmonics in the corresponding Fourier expansion] ... With a super-diode type op-amp circuit you get a complete emulation of the absolute value function as opposite to what a GreenRinger does ... if anything all the harmonics suggest that |x| is not a good approximation to x^2 (the squaring function) - which is what's achieved with a true clean octaver ... and this type clean analogue squarer can only be obtained through Gilbert multiplication - using a well-balanced circuit ...
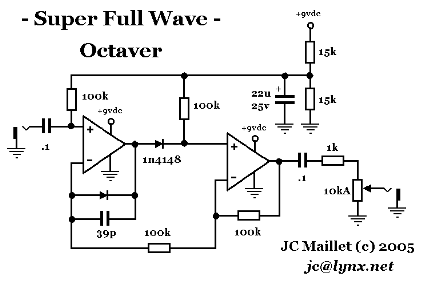 |
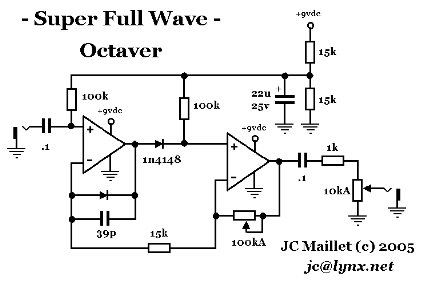
The circuit that I wired together allows for varying the second lobe from nothing to a ten-fold difference at least ... I wanted to hear what super half-wave and super full-wave sounded like against each other ... you can definitely hear a focusing of the ring when you match the 100k pot to the 15k resistor ...
 |
viva Analog /// jc -> lynx.net


